Division Euclidienne
Étant donnés deux entiers \(a\) et \(b\) avec \(b \ne 0\):
Il existe un unique couple d'entiers \(q\) et \(r\) avec:
\(a = b \times q + r\)
\(0 \le r \lt q\)
\(q\) et \(r\) sont respectivement appelés le quotient et le reste de la division Euclidienne de \(a\) par \(b\).
Exemple: 365 \(\div\) 8
\begin{array}{c|rrrr}
365 & 8\\
\hline 5 & 45 \\
\end{array}
On a bien : \(365 = 8 \times 45 + 5\) et \(0 \le 5 \lt 8\)
Attention:
on pourrait décomposer 365 autrement,
par exemple: \(365 = 8 \times 44 + 13\)
mais le fait que \(13 \ge 8\) a pour conséquence que \(365 = 8 \times 44 + 13\) n'est pas l'écriture de la division Euclienne de 365 par 8.
On retiendra
\begin{array}{c|rrrr}
Dividende & Diviseur\\
\hline Reste & Quotient \\
\end{array}
Ainsi que \(Dividende = Diviseur \times Quotient + Reste \)
avec \(0 \le Reste \lt Quotient\)
Interprétation de la division Euclidienne:
Étant donnés \(a\) objets, on cherche à faire des groupes (ou paquets) de \(b\) objets.
La division Euclidienne signifie alors qu'on peut réaliser au maximum \(q\) groupes chacun composé de \(b\) objets et il restera \(r\) objets n'étant pas assez nombreux pour former un groupe.
Définition:
Soient \(a\) et \(b\) avec \(b \ne 0\).
On dit que \(b\) est un diviseur de \(a\) si le reste de la division Euclidienne de \(a\) par \(b\) est \(0\)
En d'autres termes, \(b\) est un diviseur de \(a\) s'il existe un entier \(k\) tel que \(a = k \times b\)
Dans ce cas, on dira que \(b\) divise \(a\)
Ou encore \(b\) est un diviseur \(a\)
Ou encore que \(a\) est un multiple de \(b\)
Ou encore \(a\) est dans la table de \(b\)
les termes de vocabulaire précédents sont à connaître
Retenons qu'un diviseur de \(n\) est toujours inférieur ou égal à \(n\)
Exemples:
7 est un diviseur de 21
(\(21 = 7 \times 3\))
8 divise 80
(\(80 = 8 \times 10\))
55 est un multiple de 11
(\(55= 11 \times 5\))
Les multiples de 2 sont appelés les entiers pairs.
À retenir: On prouve que \(b\) est un diviseur de \(a\) en effectuant la division Euclidienne de \(a\) par \(b\) :
\begin{array}{c|rrrr}
55 & 11\\
\hline 0 & 5\\
\end{array}
Il reste 0 dans la division Euclidienne de 55 par 11 donc 11 divise 55.
Critères de divisibilité par 2 ; 3 ; 4 ; 5 ; 9 et 10:
a) Critère de divisibilité par 2 :
Un nombre est divisible par 2 (ou est un multiple de 2) si son chiffre des unités est 0 ; 2 ; 4 ; 6 ou 8.
Exemples : 1 798 ; 11 200 ; 145756 sont divisibles par 2
b) Critère de divisibilité par 3 :
Un nombre est divisible par 3 (ou est un multiple de 3) si la somme des chiffres qui le composent est divisible par 3.
Exemples : 12654 est divisible par 3 car 1+2+6+5+4=18 et 18 est divisible par 3 (6 × 3 = 18).
132621 est divisible par 3 car 1+3+2+6+2+1=15 et 15 est divisible par 3 (5 × 3 = 15).
c) Critère de divisibilité par 4 :
Un nombre est divisible par 4 (ou est un multiple de 4) si le nombre composé des deux derniers chiffres est divisible par 4.
Exemples :
1716 est divisible par 4 car le nombre formé des deux derniers chiffres est 16 et 16 est divisible par 4 (4 x 4 = 16)
6924 est divisible par 4 car le nombre formé des deux derniers chiffres est 24 et 24 est divisible par 4 (6 x 4 = 24)
d) Critère de divisibilité par 5 :
Un nombre est divisible par 5 (ou est un multiple de 5) si son chiffre des unités est 0 ou 5.
Exemples : 2795 ; 23200 ; 145755 sont divisibles par 5.
e) Critère de divisibilité par 9 :
Un nombre est divisible par 9 (ou est un multiple de 9) si la somme des chiffres qui le composent est divisible par 9.
Exemples :
12654 est divisible par 9 car 1+2+6+5+4 = 18 et 18 est divisible par 9 (9 x 2 = 18)
189261 est divisible par 9 car
1+8+9+2+6+1 = 27 et 27 est divisible par 9 (9 x 3 = 27)
f) critère de divisibilité par 10 :
Un nombre est divisible par 10 (ou est un multiple de 10) si son chiffre des unités est 0.
Exemple : 160 est divisible par 10 car le chiffre des unités est 0.
Propriété: Soit \(d\), \(n\) et \(m\) des entiers non nuls.
Si \(d\) divise \(n\) et \(d\) divise \(m\) alors \(d\) divise \(n + m\)
exemple: 3 divise 12 et 3 divise 24 donc 3 divise 12+24 donc 36.
Démonstration:
\(d\) divise \(n\) donc il existe un entier \(k\) tel que \(n = d \times k\)
\(d\) divise \(m\) donc il existe un entier \(k'\) tel que \(m = d \times k'\)
Ainsi \(n + m = d \times k + d \times k'\)
Donc par factorisation: \(n + m = d \times (k + k')\)
Il existe donc un entier (\(k + k'\)) tel que \(n + m = d \times (k + k')\)
donc \(d\) divise \(n + m\)
C'est cette dernière propriété qui est à la source des démonstrations des critères de divisibilité précédents par 2,3,5, 9 et 10.
Propriété: Soit \(n\) un entier non nul. \(n\) possède au moins deux diviseurs: \(1\) et \(n\)
En effet, l'écriture \(n = 1 \times n + 0\) le prouve.
En d'autres termes:
1 un diviseur à tout entier \(n\)
Pour tout \(n \ne 0\), \(n\) divise \(n\).
Liste de diviseurs d'un entier:
Il est fréquent d'avoir à établir la liste des diviseurs d'un entier.
Si l'on note D(\(n\)) la liste des diviseurs de l'entier \(n\), cette liste contient donc toujours au moins deux éléments: \(1\) et \(n\)
D(\(n\)) = {1; ... ; n}
Exemples:
La liste des diviseurs de 8 est D(\(8\)) = {1;2;4;8}
La liste des diviseurs de 14 est D(\(14\)) = {1;2;7;14}
La liste des diviseurs de 20 est D(\(14\)) = {1;2;4;5;10;20}
Lorsque cette liste est réduite à 2 éléments, l'entier \(n\) correspondant porte une dénomination toute particulière:
Définition:
On dit qu'un entier \(n\) est un nombre premier si ces seuls diviseurs sont \(1\) et \(n\)
Par convention, 1 n'est pas premier.
Exemples:
Les premiers nombres premiers sont 2;3;5;7;11;13;17; ...
2 est le premier nombre premier, c'est d'ailleurs le seul nombre premier pair.
37 et 41 sont premiers.
Cette liste est infinie: il existe une infinité de nombres premiers.
Ces nombres, qui sont tout à fait particuliers, sont les "briques" qui composent les nombres entiers.
On décompose tout nombre entier à l'aide de nombres premiers, comme on le verra par la suite.
Pour prouver qu'un nombre n'est pas premier, il suffit de trouver l'un de ces diviseurs, autres que 1 et lui-même:
Par exemple, l'égalité \(6 = 2 \times 3\) prouve que \(6\) n'est pas premier. (il existe d'autres diviseurs de 6 autres que 1 et 6)
Crible d'Ératosthène:
Liste des nombres premiers de 1 à 100:
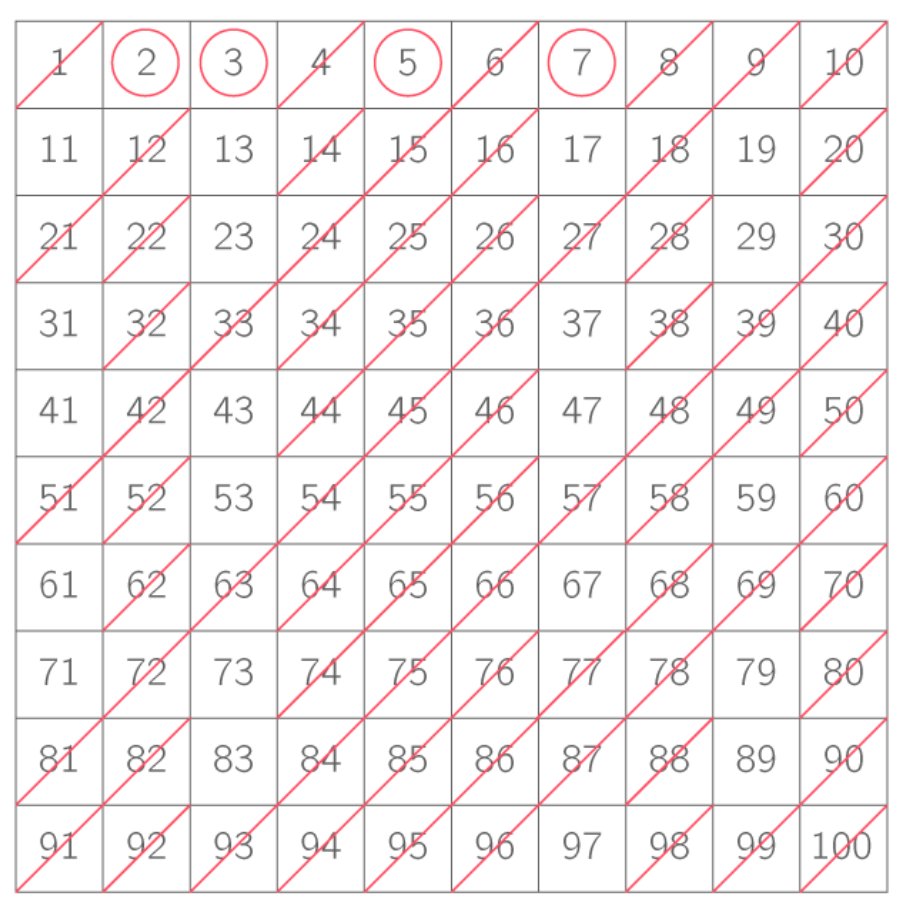
On rappelle que 1 n'est pas premier.
2 est premier. On l'indique en rouge.
Les nombres premiers plus grand que 2 ne peuvent être multiples de 2, sinon ils ne seraient pas premiers.
On barre donc les multiples de 2: (4; 6; 8; ...)
Le premier nombre qui suit et qui n'est pas barré est 3.
3 est premier. Les nombres premiers plus grand que 3 ne peuvent être multiples de 3, sinon ils ne seraient pas premiers.
On barre donc les multiples de 3 (6; 9; 12; ...), ou du moins ceux qui ne sont pas déjà barrés.
Le premier nombre qui suit et qui n'est pas barré est 5.
5 est premier. Les nombres premiers plus grand que 5 ne peuvent être multiples de 5, sinon ils ne seraient pas premiers.
On barre donc les multiples de 5 (10 qui est déjà barré; 15 aussi; 20 idem; 25...)
À la fin du processus, tous les entiers qui n'ont pas été rayés sont les nombres premiers inférieurs à 100.
A faire:
Décomposition en facteurs premiers
Simplification de fractions