1) Grandeurs simples
a) Les grandeurs simples étudiées et leurs unités sont les suivantes:
| Grandeur | Unité | Notation |
|---|---|---|
| Longueur | Mètre | m |
| Temps | Seconde | s |
| Masse | Gramme | g |
| Tension électrique | Volt | V |
| Intensité électrique | Ampère | A |
| Puissance | Watt | W |
Les unités de longueur usuelles sont le millimètre, le centimètre, le mètre, le kilomètre ...
Les unités de temps usuelles sont la seconde, la minute, l'heure, la journée, l'année, le siècle ...
Les unités de masses usuelles sont le gramme, le kilogramme, le quintal, la tonne ...
Les unités de puissance usuelles sont le W, le kilowatt ...
Pour les conversions d'unités hors unité de temps, de grandeurs simples, on utilisera le tableau suivant
| k... (kilo) | h... (hecto) | da... (déca) | ... | d... (déci) | c... (centi) | m... (milli) |
Dans ce tableau, ... peut être remplacé par m, g, V, A pour les unités de longueur, masse, tension ou intensité.
Concernant les unités de temps, on retiendra:
- 1 min = 60 s
- 1h = 60 min = 3600 s
- 1 jour = 24 h = 24x3600 s (= 86 400 s)
- 1 année = 365 jours
- 1 siècle = 100 ans
b) Exemples
- 25 km = 25 000 m.
- 250 kV = 250 000 V
- 2000 mA = 2 A
- 12 000 V = 12 KV
- Convertir 25 m en km:
| km (kilomètres) | hm (hectomètres) | dam (décamètres) | m (mètres) | dm (décimètres) | cm (centimètres) | mm (millimètres) |
0 | 0 | 2 | 5 | |||
On placer le chiffre des unités de 25m dans la colonne des mètres (m), on complète par des zéros, puis on place la virgule à droite du chiffre obtenu dans la colonne des kilomètres.
convertir des durée données en heures et minutes en minutes:
- Convertir 5 h 41 min en minutes.
5 h 41 min = 5x60 min + 41 min = 300 min + 41 min = 341 min.
convertir des durées en heures décimales:
- Convertir 3h25min en heures décimales
On convertit tout d'abord 3h25min en minutes
3 h 25 min = 4x60 min + 25 min = 240 min + 25 min = 265 min
puis utiliser le tableau de proportionnalité suivant:
↓ x60
| Heures | 1 | ? | ↑ ÷60 |
| min | 60 | 265 |
? = 265/60 ≈ 3,417 h
- Convertir 5,67 h en heures minutes secondes
5,67 h = 5h + 0,67 h : il y a donc 5h et 0,67 h
↓ x60
| Heures | 1 | 0,67 | ↑ ÷60 |
min | 60 | ? |
0,67 h = 0,67x60 min = 40,2 min : il y a donc 40min
↓ x60
| min | 1 | 0,2 | ↑ ÷60 |
s | 60 | ? |
0,2 s = 0,2 x 60 s = 12 s
5,67 h font donc 5h 40 min et 12 s
2) Grandeurs composées
Les grandeurs composées sont des produits (résultats d'une ou plusieurs multiplication(s)) ou des quotients (résultats d'une division)
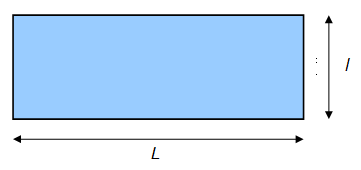
a) Aire du rectangle
L'aire d'un rectangle est le produit de sa longueur par sa largeur.
Si chaque dimension est donnée en mètres, l'unité d'aire (ou de surface) est alors le m² (mètre carré)
Aire(rectangle) = L x l
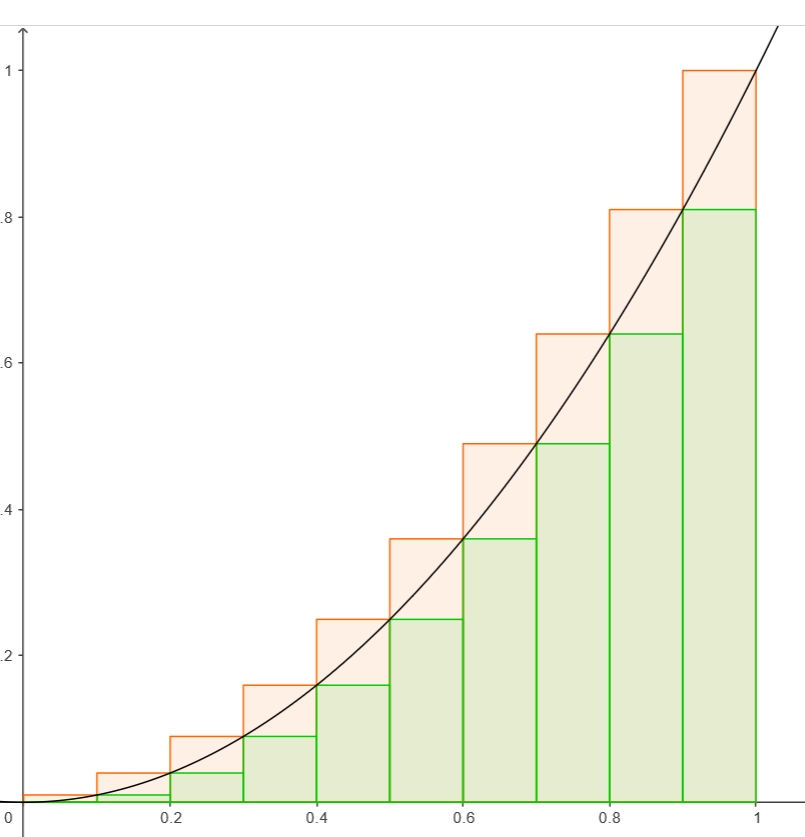
Le schéma suivant permet d'encadrer une aire "complexe" à l'aide de rectangles
b) Volume du parallélépipède rectangle
Le volume d'un parallélépipède rectangle est le produit de sa longueur par sa largeur par sa hauteur.
Si chaque dimension est donnée en mètres, l'unité d'aire (ou de surface) est alors le m3 (mètre cube)
Volume(parallélépipède) = L x l x h
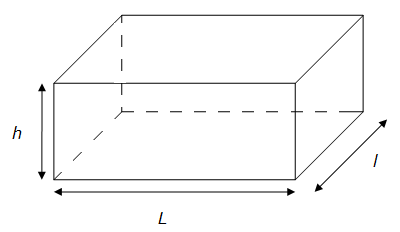
Remarquons que l'aire enveloppant le parallélépipède est A = 2(L+l+h)
c) Énergie :
L’Énergie E est le produit de la puissance par le temps:
Si P est donnée en Watts et t en heures, E a pour unité le Watt Heure (Wh)
E = P x t
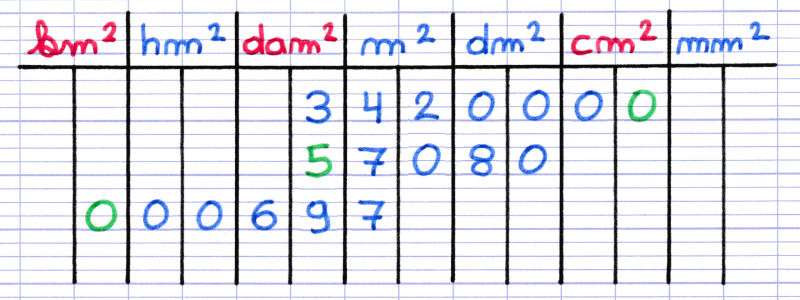
Conversions des unités d'aires et de volumes:
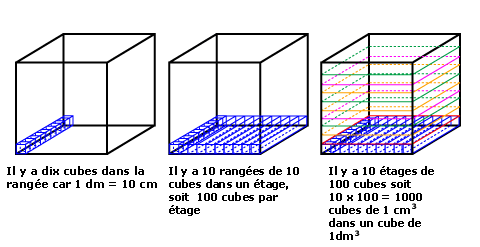
Cette figure permet de comprendre pourquoi chaque colonne du tableau de conversion des unités d'aires comporte deux sous colonnes
1dm² = 100 cm²
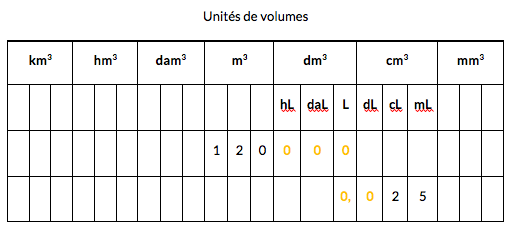
et pourquoi chaque colonne du tableau de conversion des unités de volumes comporte 3 sous colonnes.
1dm3 = 1 000 cm3
1dm3 = 1 Litre (1 L)
a) grandeurs quotients: Vitesse, Masse volumique, Débit, Densité de population